Abstraction
Note
Objective of the abstraction is to separate the parallelization strategy from the algorithm itself. Algorithm code written by users should not depend on any parallelization library or specific strategy. This would enable exchanging the parallelization back-end without any changes to the algorithm itself. Besides allowing to test different parallelization strategies this also makes it possible to port algorithms to new, yet unsupported, platforms.
Parallelism and memory hierarchies at all levels need to be exploited in order to achieve performance portability across various types of accelerators. Within this chapter an abstraction will be derive that tries to provide a maximum of parallelism while simultaneously considering implementability and applicability in hardware.
Looking at the current HPC hardware landscape, we often see nodes with multiple sockets/processors extended by accelerators like GPUs or Intel Xeon Phi, each with their own processing units. Within a CPU or a Intel Xeon Phi there are cores with hyper-threads, vector units and a large caching infrastructure. Within a GPU there are many small cores and only few caches. Each entity in the hierarchy has access to different memories. For example, each socket / processor manages its RAM, while the cores additionally have non-explicit access to L3, L2 and L1 caches. On a GPU there are global, constant, shared and other memory types which all can be accessed explicitly. The interface has to abstract from these differences without sacrificing speed on any platform.
A process running on a multi-socket node is the largest entity within alpaka. The abstraction is only about the task and data parallel execution on the process/node level and down. It does not provide any primitives for inter-node communication. However, such libraries can be combined with alpaka.
An application process always has a main thread and is by definition running on the host. It can access the host memory and various accelerator devices. Such accelerators can be GPUs, Intel Xeon Phis, the host itself or other devices. Thus, the host not necessarily has to be different from the accelerator device used for the computations. For instance, an Intel Xeon Phi simultaneously can be the host and the accelerator device.
The alpaka library can be used to offload the parallel execution of task and data parallel work simultaneously onto different accelerator devices.
Task Parallelism
One of the basic building blocks of modern applications is task parallelism. For example, the operating system scheduler, deciding which thread of which process gets how many processing time on which CPU core, enables task parallelism of applications. It controls the execution of different tasks on different processing units. Such task parallelism can be, for instance, the output of the progress in parallel to a download. This can be implemented via two threads executing two different tasks.
The valid dependencies between tasks within an application can be defined as a DAG (directed acyclic graph) in all cases. The tasks are represented by nodes and the dependencies by edges. In this model, a task is ready to be executed if the number of incoming edges is zero. After a task finished it’s work, it is removed from the graph as well as all of it’s outgoing edges,. This reduces the number of incoming edges of subsequent tasks.
The problem with this model is the inherent overhead and the missing hardware and API support. When it is directly implemented as a graph, at least all depending tasks have to be updated and checked if they are ready to be executed after a task finished. Depending on the size of the graph and the number of edges this can be a huge overhead.
OpenCL allows to define a task graph in a somewhat different way.
Tasks can be enqueued into an out-of-order command queue combined with events that have to be finished before the newly enqueued task can be started.
Tasks in the command queue with unmet dependencies are skipped and subsequent ones are executed.
The CL_QUEUE_OUT_OF_ORDER_EXEC_MODE_ENABLE property of a command queue is an optional feature only supported by few vendors.
Therefore, it can not be assumed to be available on all systems.
CUDA on the other hand does currently (version 7.5) not support such out-of-order queues in any way. The user has to define dependencies explicitly through the order the tasks are enqueued into the queues (called queues in CUDA). Within a queue, tasks are always executed in sequential order, while multiple queues are executed in parallel. Queues can wait for events enqueued into other queues.
In both APIs, OpenCL and CUDA, a task graph can be emulated by creating one queue per task and enqueuing a unique event after each task, which can be used to wait for the preceding task. However, this is not feasible due to the large queue and event creation costs as well as other overheads within this process.
Therefore, to be compatible with a wide range of APIs, the interface for task parallelism has to be constrained. Instead of a general DAG, multiple queues of sequentially executed tasks will be used to describe task parallelism. Events that can be enqueued into the queues enhance the basic task parallelism by enabling synchronization between different queues, devices or the host threads.
Data Parallelism
In contrast to task parallelism, data parallelism describes the execution of one and the same task on multiple, often related data elements. For example, an image color space conversion is a textbook example of a data parallel task. The same operation is executed independently on each pixel. Other data parallel algorithms additionally introduce dependencies between threads in the input-, intermediate-, or output-data. For example, the calculation of a brightness histogram has no input-data dependencies. However, all pixel brightness values finally have to be merged into a single result. Even these two simple examples show that it is necessary to think about the interaction of parallel entities to minimize the influence of data dependencies.
Furthermore, it is necessary to respect the principles of spatial and temporal locality. Current hardware is built around these locality principles to reduce latency by using hierarchical memory as a trade-off between speed and hardware size. Multiple levels of caches, from small and very fast ones to very large and slower ones exploit temporal locality by keeping recently referenced data as close to the actual processing units as possible. Spatial locality in the main memory is also important for caches because they are usually divided into multiple lines that can only be exchanged one cache line at a time. If one data element is loaded and cached, it is highly likely that nearby elements are also cached. If the pixels of an image are stored row wise but are read out column wise, the spatial locality assumption of many CPUs is violated and the performance suffers. GPUs on the other hand do not have a large caching hierarchy but allow explicit access to a fast memory shared across multiple cores. Therefore, the best way to process individual data elements of a data parallel task is dependent on the data structure as well as the underlying hardware.
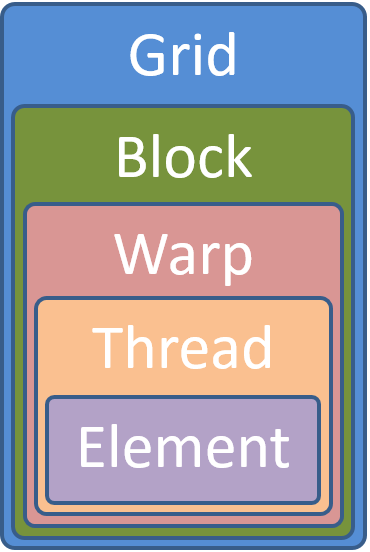
The main part of the alpaka abstraction is the way it abstracts data parallelism and allows the algorithm writer to take into account the hierarchy of processing units, their data parallel features and corresponding memory regions. The abstraction developed is influenced and based on the groundbreaking CUDA and OpenCL abstractions of a multidimensional grid of threads with additional hierarchy levels in between. Another level of parallelism is added to those abstractions to unify the data parallel capabilities of modern hardware architectures. The explicit access to all hierarchy levels enables the user to write code that runs performant on all current platforms. However, the abstraction does not try to automatically optimize memory accesses or data structures but gives the user full freedom to use data structures matching the underlying hardware preferences.
Thread
Theoretically, a basic data parallel task can be executed optimally by executing one thread per independent data element. In this context, the term thread does not correspond to a native kernel-thread, an OpenMP thread, a CUDA thread, a user-level thread or any other such threading variant. It only represents the execution of a sequence of commands forming the desired algorithm on a per data element level. This ideal one-to-one mapping of data elements to threads leads to the execution of a multidimensional grid of threads corresponding to the data structure of the underlying problem. The uniform function executed by each of the threads is called a kernel. Some algorithms such as reductions require the possibility to synchronize or communicate between threads to calculate a correct result in a time optimal manner. Therefore our basic abstraction requires a n-dimensional grid of synchronizable threads each executing the same kernel. The following figure shows an hypothetical processing unit that could optimally execute this data parallel task. The threads are mapped one-to-one to the cores of the processor. For a time optimal execution, the cores have to have an all-to-all equal length connection for communication and synchronization.
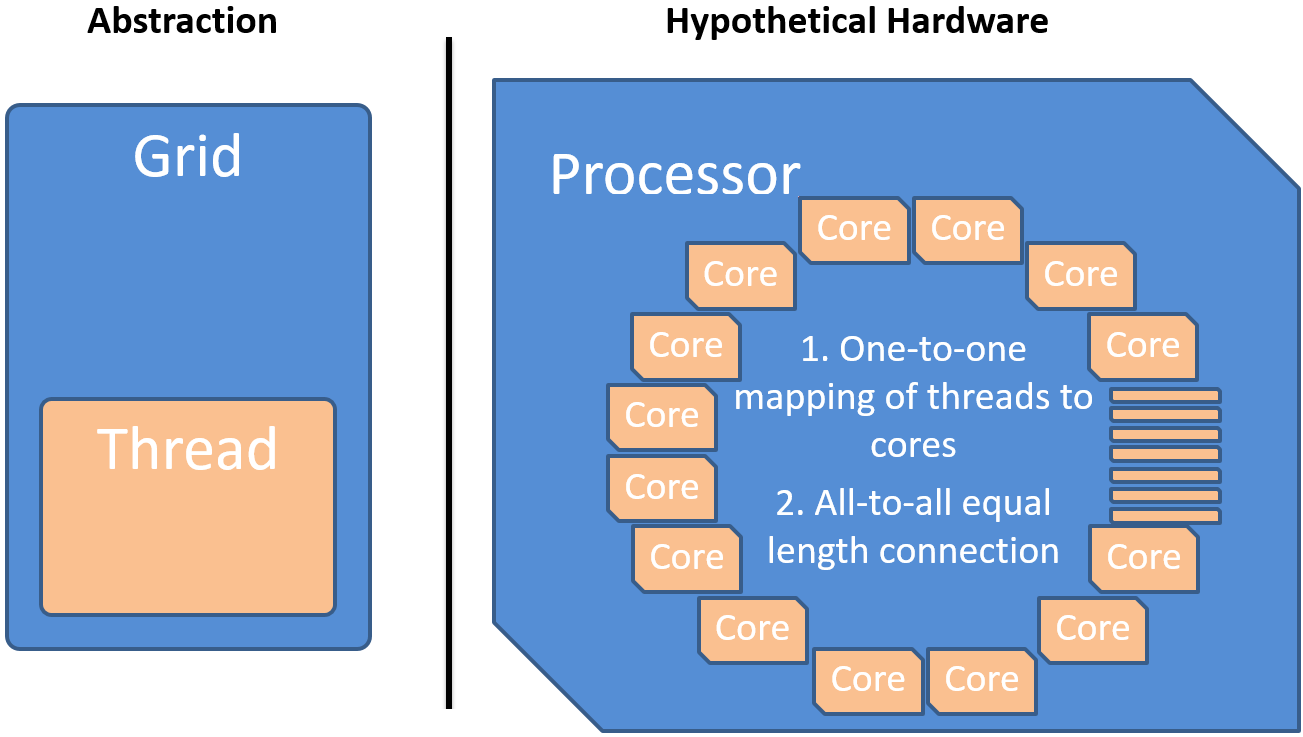
The only difference between the threads is their positional index into the grid which allows each thread to compute a different part of the solution. Threads can always access their private registers and the global memory.
Registers
All variables with default scope within a kernel are automatically saved in registers and are not shared automatically. This memory is local to each thread and can not be accessed by other threads.
Global Memory
The global memory can be accessed from every thread in the grid as well as from the host thread. This is typically the largest but also the slowest memory available.
Individual threads within the grid are allowed to statically or dynamically allocate buffers in the global memory.
Prior to the execution of a task, the host thread copies the input buffers and allocates the output buffers onto the accelerator device. Pointers to these buffers then can be given as arguments to the task invocation. By using the index of each thread within the grid, the offset into the global input and output buffers can be calculated. After the computation has finished, the output buffer can be used either as input to a subsequent task or can be copied back to the host.
Block
Building a processor with possibly thousands of cores where all cores have an equal length connection for fast communication and synchronization is not viable. Either the processor size would have to grow exponentially with the number of cores or the all-to-all communication speed would decrease so much that computations on the processor would be impractical. Therefore, the communication and synchronization of threads has to be limited to sizes manageable by real hardware.
Figure ref{fig:block} depicts the solution of introducing a new hierarchy level in the abstraction. A hypothetical processor is allowed to provide synchronization and fast communication within blocks of threads but is not required to provide synchronization across blocks. The whole grid is subdivided into equal sized blocks with a fast but small shared memory. Current accelerator abstractions (CUDA and OpenCL) only support equal sized blocks. This restriction could possibly be lifted to support future accelerators with heterogeneous block sizes.
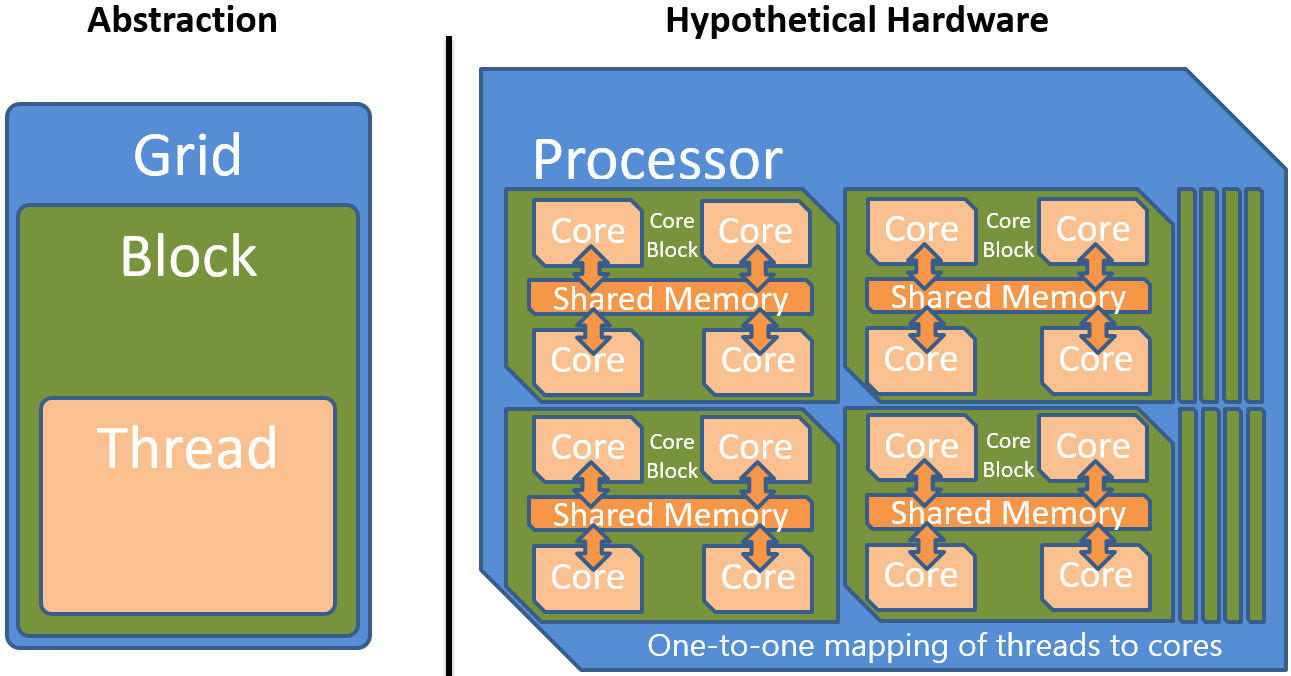
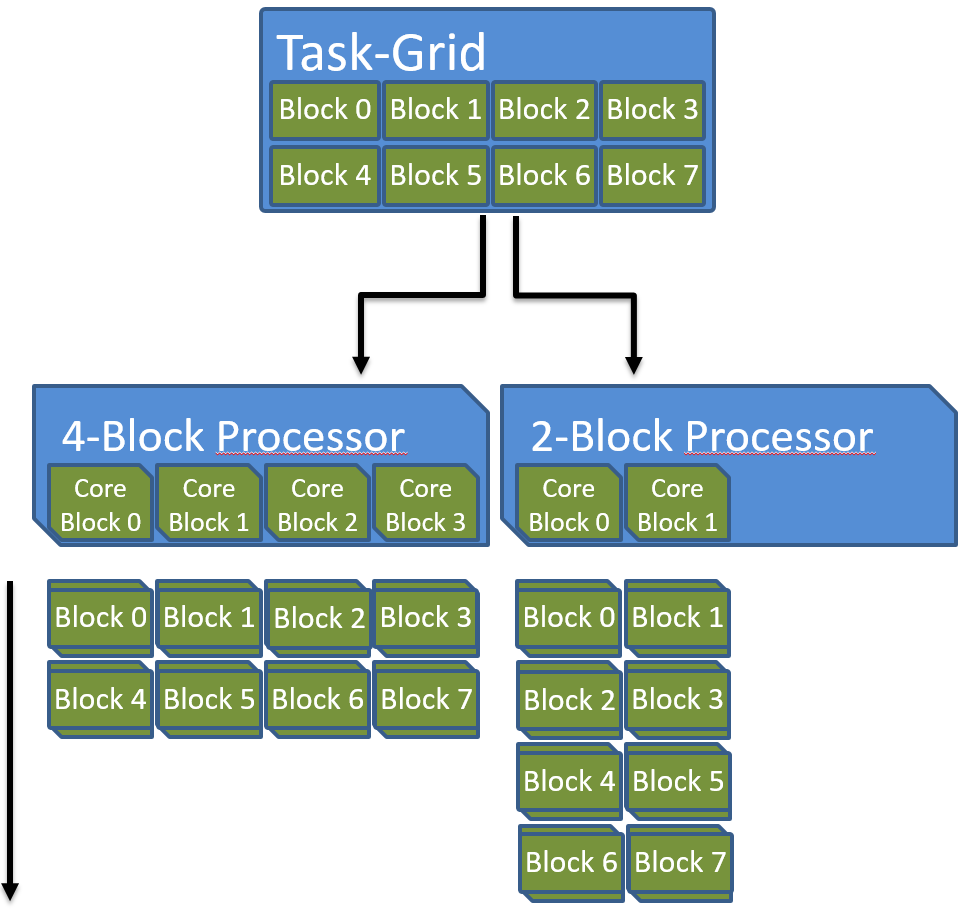
There is another reason why independent blocks are necessary. Threads that can communicate and synchronize require either a one-to-one mapping of threads to cores, which is impossible because the number of data elements is theoretically unlimited, or at least a space to store the state of each thread. Even old single core CPUs were able to execute many communicating and synchronizing threads by using cooperative or preemptive multitasking. Therefore, one might think that a single core would be enough to execute all the data parallel threads. But the problem is that even storing the set of registers and local data of all the possible millions of threads of a task grid is not always viable. The blocking scheme solves this by enabling fast interaction of threads on a local scale but additionally removes the necessity to store the state of all threads in the grid at once because only threads within a block must be executed in parallel. Within a block of cores there still has to be enough memory to store all registers of all contained threads. The independence of blocks allows applications to scale well across diverse devices. As can be seen in the following figure, the accelerator can assign blocks of the task grid to blocks of cores in arbitrary order depending on availability and workload.
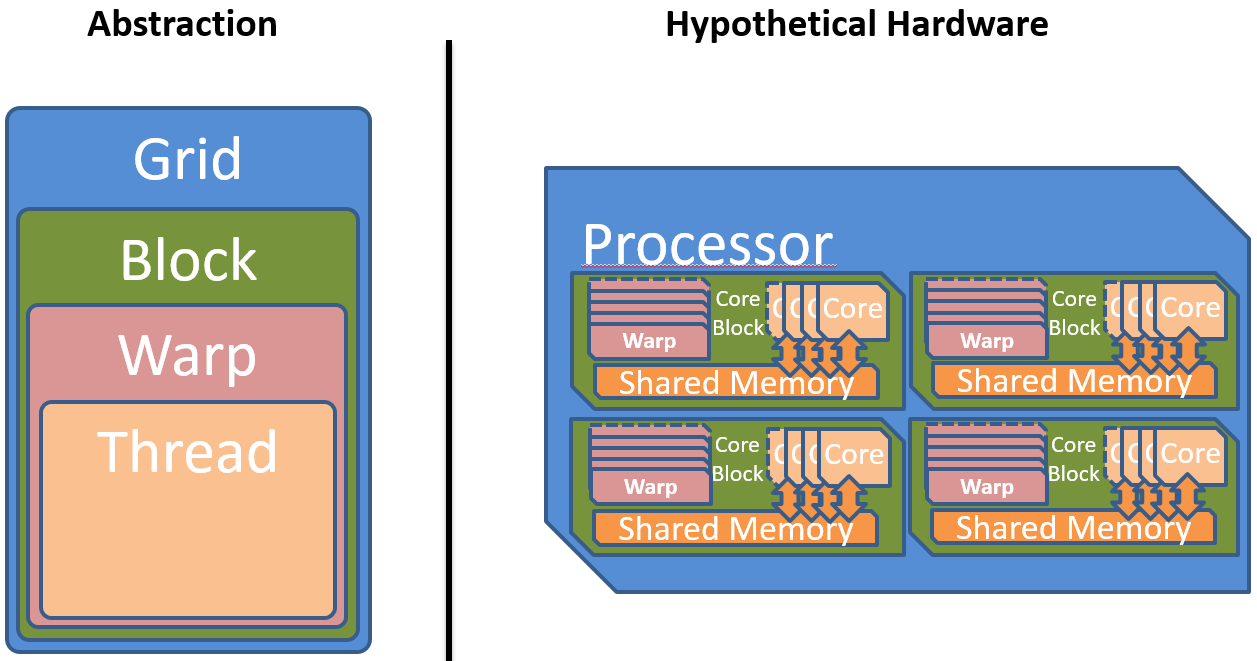
Warp
With the current abstraction only independent parallelism via blocks and synchronizable parallelism via threads can be expressed. However, there are more variants of parallelism in real hardware. Because all threads in the grid are executing the same kernel and even the same instruction at the same time when ignoring divergent control flows, a lot of chip space can be saved. Multiple threads can be executed in perfect synchronicity, which is also called lock-step. A group of such threads executing the same instruction at the same time is called a warp . All threads within a warp share a single instruction pointer (IP), and all cores executing the threads share one instruction fetch (IF) and instruction decode (ID) unit.
Even threads with divergent control flows can be executed within one warp. CUDA, for example, solves this by supporting predicated execution and warp voting. For long conditional branches the compiler inserts code which checks if all threads in the warp take the same branch. For small branches, where this is too expensive, all threads always execute all branches. Control flow statements result in a predicate and only in those threads where it is true, the predicated instructions will have an effect.
Not only CUDA GPUs support the execution of multiple threads in a warp. Full blown vector processors with good compilers are capable of combining multiple loop iterations containing complex control flow statements in a similar manner as CUDA.
Due to the synchronitiy of threads within a warp, memory operations will always occur at the same time in all threads. This allows to coalesce memory accesses. Different CUDA devices support different levels of memory coalescing. Older ones only supported combining multiple memory accesses if they were aligned and sequential in the order of thread indices. Newer ones support unaligned scattered accesses as long as they target the same 128 byte segment.
The ability of very fast context switches between warps and a queue of ready warps allows CUDA capable GPUs to hide the latency of global memory operations.
Element
To use the maximum available computing power of, for example, a modern x86 processor, the computation has to utilize the SIMD vector registers. Many current architectures support issuing a single instruction that can be applied to multiple data elements in parallel.
The original x86 instruction set architecture did not support SIMD instructions but has been enhanced with MMX (64 bit width registers), SSE (128 bit width registers), AVX (256 bit width registers) and AVX-512 (512 bit width registers) extensions. In varying degree, they allow to process multiple 32 bit and 64 bit floating point numbers as well as 8, 16, 32 and 64 bit signed and unsigned integers.
CUDA capable GPUs do not have vector registers where multiple values of type float or double can be manipulated by one instruction.
Nevertheless, newer CUDA capable devices implement basic SIMD instructions on pairs of 16 bit values and quads of 8-bit values.
They are described in the documentation of the PTX instruction set architecture chapter 9.7.13 but are only of any use in very special problem domains, for example for deep learning.
It would be optimal if the compiler could automatically vectorize our kernels when they are called in a loop and vectorization is supported by the underlying accelerator.
However, besides full blown vector processors, mainstream CPUs do not support predicated execution or similar complex things within vector registers.
At most, there is support for masking operations which allow to emulate at least some conditional branching.
Therefore, this missing hardware capability has to be circumvented by the compiler.
There are scientific research projects such as the work done by Ralf Karrenberg et al [1, 2, 3 ] building on the LLVM compiler infrastructure supporting such whole-function vectorization.
However, current mainstream compilers do not support automatic vectorization of basic, non trivial loops containing control flow statements (if, else, for, etc.) or other non-trivial memory operations.
Therefore, it has to be made easier for the compiler to recognize the vectorization possibilities by making it more explicit.
The opposite of automatic whole function vectorization is the fully explicit vectorization of expressions via compiler intrinsics directly resulting in the desired assembly instruction.
A big problem when trying to utilize fully explicit vectorization is, that there is no common foundation supported by all explicit vectorization methods.
A wrapper unifying the x86 SIMD intrinsics found in the intrin.h or x86intrin.h headers with those supported on other platforms, for example ARM NEON (arm_neon.h), PowerPC Altivec (altivec.h) or CUDA is not available and to write one is a huge task in itself.
However, if this would become available in the future, it could easily be integrated into alpaka kernels.
Due to current compilers being unable to vectorize whole functions and the explicit vectorization intrinsics not being portable, one has to rely on the vectorization capabilities of current compilers for primitive loops only consisting of a few computations. By creating a grid of data elements, where multiple elements are processed per thread and threads are pooled in independent blocks, as it is shown in the figure below, the user is free to loop sequentially over the elements or to use vectorization for selected expressions within the kernel. Even the sequential processing of multiple elements per thread can be useful depending on the architecture. For example, the NVIDIA cuBLAS general matrix-matrix multiplication (GEMM) internally executes only one thread for each second matrix data element to better utilize the registers available per thread.
Note
The best solution to vectorization would be one, where the user does not have to do anything. This is not possible because the smallest unit supplied by the user is a kernel which is executed in threads which can synchronize.
It is not possible to execute multiple kernels sequentially to hide the vectorization by starting a kernel-thread for e.g. each 4th thread in a block and then looping over the 4 entries. This would prohibit the synchronization between these threads. By executing 4 fibers inside such a vectorization kernel-thread we would allow synchronization again but prevent the loop vectorizer from working.
Summary
This abstraction is called Redundant Hierarchical Parallelism. This term is inspired by the paper The Future of Accelerator Programming: Abstraction, Performance or Can We Have Both? PDF DOI It investigates a similar concept of copious parallel programming reaching 80%-90% of the native performance while comparing CPU and GPU centric versions of an OpenCL n-body simulation with a general version utilizing parallelism on multiple hierarchy levels.
The CUDA or OpenCL abstractions themselves are very similar to the one designed in the previous sections and consists of all but the Element level. However, as has been shown, all five abstraction hierarchy levels are necessary to fully utilize current architectures. By emulating unsupported or ignoring redundant levels of parallelism, algorithms written with this abstraction can always be mapped optimally to all supported accelerators. The following table summarizes the characteristics of the proposed hierarchy levels.
Hierarchy Level
Parallelism
Synchronizable
—
—
—
grid
sequential / parallel
– / X
block
parallel
–
warp
parallel
X
thread
parallel / lock-step
X
element
sequential
–
Depending on the queue a task is enqueued into, grids will either run in sequential order within the same queue or in parallel in different queues. They can be synchronized by using events. Blocks can not be synchronized and therefore can use the whole spectrum of parallelism ranging from fully parallel up to fully sequential execution depending on the device. Warps combine the execution of multiple threads in lock-step and can be synchronized implicitly by synchronizing the threads they contain. Threads within a block are executed in parallel warps and each thread computes a number of data elements sequentially.